Data Structures – Min / Max Heap

I’m King of the Hill, Top of the Heap

I’m going to briefly break away from WPF / MVVM development to look at a data structure that will be required for the next post.

The System.Collections.Generic namespace contains many collection classes – List, Stack, Queue, Hashset, Dictionary etc – but these aren’t always suitable for all requirements. In this case, I needed a priority queue. This works like a regular queue, with add and remove operations, except that the items are ranked with the best one moved to the front of the queue, regardless of the order in which they were added – much like those front of line passes that amusement parks sell. There is no requirement for sorting the remaining items, so a fully sorted data structure such as a red-black tree is overkill. However, depending on the implementation used for the priority queue, the items may be arranged in some defined order for efficient processing. New items can be added to the queue, updating the best item as appropriate, whilst the queue is being processed. An example of this usage is building a Huffman encoding tree.

There are several different ways to implement a priority queue. As my current requirement is to hold a relatively small number of items in the queue, I’ve gone for the one that’s easiest to code without worrying too much about finding absolute optimal performance – a binary heap. Binary heaps exist in two flavours – min-heap & max-heap, the only difference being whether it’s the lowest ranked item or the highest that is considered best and held at the top of the heap.

A binary heap is defined as a binary tree with two constraints

1. The tree is complete – all levels of the tree (except possibly the last one) are full, and if it’s not full then the lowest level is filled from left to right.
2. Each node in the tree is ordered so that it ranks better that any child nodes it may have.

Note that other than to satisfy heap constraint 2, there is no other ordering of items, either on the same level or between levels. Organising the tree in this way is much more efficient than scanning the whole collection to find the best value each time – O(log n) vs O(n).

By default, a binary heap is not stable – the order in which items with the same priority will be returned is not defined, and will vary depending on what other items have already been added to the heap. If stability is a requirement, then you have to include an indexing or time-stamp value in the item sort order.

For a given set of items, there are many arrangements of the heap that satisfy the two constraints. The exact structure depends on the order that the items are added to the heap.

An example min-heap structure …

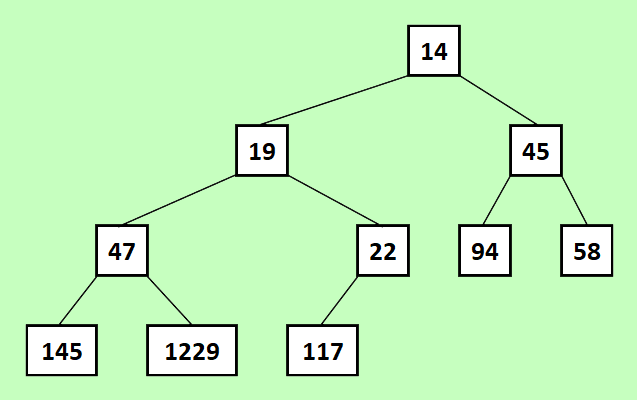
The easiest implementation for a binary heap is using an array – the best item is held in index zero. Two operations are required for the heap.

• Add – The new item is added to the first unused element of the array, expanding the array if required, and increasing the item count. The heap is then re-organised, starting from the newly added element, comparing it to its parent, and swapping if necessary. This process continues up the tree, so long as a swap was required, until we reach item index zero. This will eventually move the best item to top of the heap, if it’s not already there.

  // Add a new item to the heap, then rearrange the items so that the highest / lowest item is at the top
  public void Add(T item)
  {
      // grow the heap array if necessary
      if (Count == _capacity)
      {
          _capacity = _capacity * 2 + 1;
          var newHeap = new T[_capacity];
          Array.Copy(Heap, 0, newHeap, 0, Count);
          Heap = newHeap;
      }
  
      Heap[Count] = item;
      Count++;
  
      FixHeapAfterAdd();
  }
  
  // The new item was added in last element of array (index = Count-1)
  // Now rearrange the heap, staring from the last item, so that each parent node is sorted higher than both of its children
  private void FixHeapAfterAdd()
  {
      var currentIndex = Count - 1;
      while (currentIndex > 0)
      {
          var parentIndex = (currentIndex - 1) / 2;
          var compare = Heap[currentIndex].CompareTo(Heap[parentIndex]);
  
          if ((_heapType == HeapType.Min && compare < 0) || (_heapType == HeapType.Max && compare > 0))
          {
              SwapItems(parentIndex, currentIndex);
              currentIndex = parentIndex;
          }
          else
              break;
      }
  }
  

• Remove – The current best item is swapped with the last item in the array, and then effectively discarded as the item count is reduced by one. The heap is then re-organised starting from index zero. The item currently in index zero (which will be out of place as it was previously at the bottom of the heap) is compared with its children, swapping to promote the best of the three items to that slot. So long as a swap is required, this process is repeated with the demoted item. This will advance the new best item to the top of the heap (index zero).

  Note that by rule, the two items in level 1 (array indexes 1 & 2) each rank better than all of their children, and so one of these will be the new best item in the heap.

  // Return the highest / lowest value from the top of the heap, then re-arrange the remaining
  // items so that the next highest / lowest item is moved to the top.
  public T Remove()
  {
      if (Count == 0)
          throw new InvalidOperationException($"{nameof(Remove)}() called on an empty heap");
  
      var result = Heap[0];
  
      Count--;
      if (Count > 0)
          SwapItems(0, Count);
  
      Heap[Count] = default(T);
      FixHeapAfterRemove();
  
      return result;
  }
  
  // The Last item in the heap was swapped with the removed item (index 0), which is then effectively discarded as the heap count is reduced by 1.
  // Now rearrange the heap, starting from the top item, comparing it to each of its children, swapping to promote the best to that slot.
  // Repeat as necessary with the demoted item.
  private void FixHeapAfterRemove()
  {
      var currentIndex = 0;
  
      // Keep walking down the heap, placing best of three items (current + its two children) in highest position, so long as a swap is required            
      while (true)
      {
          var bestItemIndex = currentIndex;
          var leftChildIndex = currentIndex * 2 + 1;
          var rightChildIndex = currentIndex * 2 + 2;
  
          if (leftChildIndex < Count)
          {
              var compare = Heap[leftChildIndex].CompareTo(Heap[currentIndex]);
              if ((_heapType == HeapType.Min && compare < 0) || (_heapType == HeapType.Max && compare > 0))
                  bestItemIndex = leftChildIndex;
          }
  
          if (rightChildIndex < Count)
          {
              var compare = Heap[rightChildIndex].CompareTo(Heap[bestItemIndex]);
              if ((_heapType == HeapType.Min && compare < 0) || (_heapType == HeapType.Max && compare > 0))
                  bestItemIndex = rightChildIndex;
          }
  
          if (bestItemIndex == currentIndex)
              break;
  
          SwapItems(currentIndex, bestItemIndex);
          currentIndex = bestItemIndex;
      }
  }
  

The demo project for this post shows both a min-heap and max-heap in action. A set of integers are added in random order, showing the state of the heap after each step, and then removed again in sorted order. For those of you racking your brains trying to work out what the numbers represent, they’re just the house numbers of the various properties I’ve lived in over the years, in chronological order.

In my next post, I’ll return to WPF behaviors – showing the max-heap in action as I demonstrate a methodology for enhancing the TreeView control.

Don’t forget that all of the code samples for this blog are available on Github, along with my own personal C# / WPF library.

If you find this article useful, or you have any other feedback, please leave a comment below.